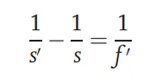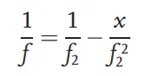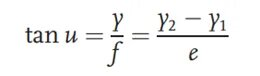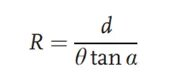Definisjon og testmetoder for brennvidde for optiske systemer

1. Brennvidde for optiske systemer

Brennvidde er en svært viktig indikator på det optiske systemet. For konseptet brennvidde har vi mer eller mindre en forståelse av det, og vi gjennomgår det her.
Brennvidden til et optisk system, definert som avstanden fra det optiske sentrum i det optiske systemet til strålens fokus når parallelt lys faller inn, er et mål på konsentrasjonen eller divergensen av lys i et optisk system. Vi bruker følgende diagram for å illustrere dette konseptet.

I figuren ovenfor konvergerer den parallelle strålen som innfaller fra venstre ende, etter å ha passert gjennom det optiske systemet, mot bildefokus F'. Den reverserte forlengelseslinjen til den konvergerende strålen skjærer den tilsvarende forlengelseslinjen til den innfallende parallelle strålen i et punkt. Flaten som passerer dette punktet og er vinkelrett på den optiske aksen kalles det bakre hovedplanet. Det bakre hovedplanet skjærer den optiske aksen i punkt P2, som kalles hovedpunktet (eller det optiske midtpunktet). Avstanden mellom hovedpunktet og bildefokuset er det vi vanligvis kaller brennvidden. Det fulle navnet er bildets effektive brennvidde.
Det kan også sees fra figuren at avstanden fra den siste overflaten av det optiske systemet til fokuspunktet F' på bildet kalles bakre brennvidde (BFL). Tilsvarende, hvis den parallelle strålen faller inn fra høyre side, finnes det også konsepter for effektiv brennvidde og fremre brennvidde (FFL).

2. Metoder for testing av brennvidde

I praksis finnes det mange metoder som kan brukes til å teste brennvidden til optiske systemer. Basert på ulike prinsipper kan metodene for testing av brennvidde deles inn i tre kategorier. Den første kategorien er basert på bildeplanets posisjon, den andre kategorien bruker forholdet mellom forstørrelse og brennvidde for å finne brennviddeverdien, og den tredje kategorien bruker bølgefrontkrumningen til den konvergerende lysstrålen for å finne brennviddeverdien.
I denne delen vil vi introdusere de vanligste metodene for testing av brennvidden til optiske systemer:

2.1Collimatormetoden

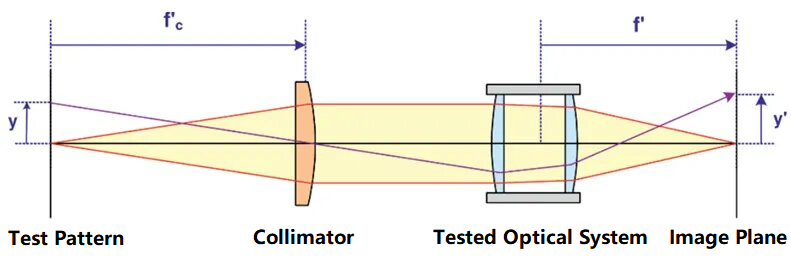
Prinsippet for å bruke en kollimator til å teste brennvidden til et optisk system er vist i diagrammet nedenfor:

I figuren er testmønsteret plassert i kollimatorens fokus. Høyden y på testmønsteret og brennvidden f_c' til kollimatoren er kjent. Etter at den parallelle strålen som sendes ut av kollimatoren er konvergert av det testede optiske systemet og avbildet på bildeplanet, kan brennvidden til det optiske systemet beregnes basert på høyden y' til testmønsteret på bildeplanet. Brennvidden til det testede optiske systemet kan bruke følgende formel:

2.2 GaussiskMmetode
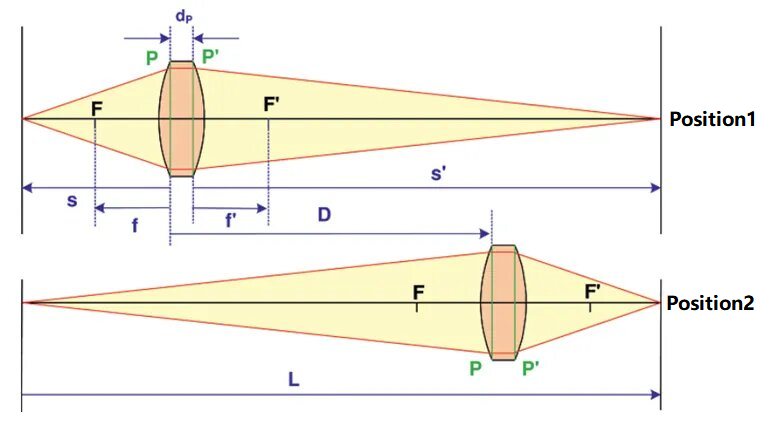
Den skjematiske figuren av Gauss-metoden for å teste brennvidden til et optisk system er vist nedenfor:

I figuren er de fremre og bakre hovedplanene til det optiske systemet som testes representert som henholdsvis P og P', og avstanden mellom de to hovedplanene er d_PI denne metoden er verdien av d_Panses å være kjent, eller verdien er liten og kan ignoreres. Et objekt og en mottakerskjerm plasseres i venstre og høyre ende, og avstanden mellom dem registreres som L, hvor L må være større enn 4 ganger brennvidden til systemet som testes. Systemet som testes kan plasseres i to posisjoner, betegnet som henholdsvis posisjon 1 og posisjon 2. Objektet til venstre kan avbildes tydelig på mottakerskjermen. Avstanden mellom disse to stedene (betegnet som D) kan måles. I henhold til konjugerforholdet kan vi få:

På disse to posisjonene registreres objektavstandene som henholdsvis s1 og s2, da er s2 - s1 = D. Ved å utlede formelen kan vi få brennvidden til det optiske systemet som vist nedenfor:

2.3Lensometer
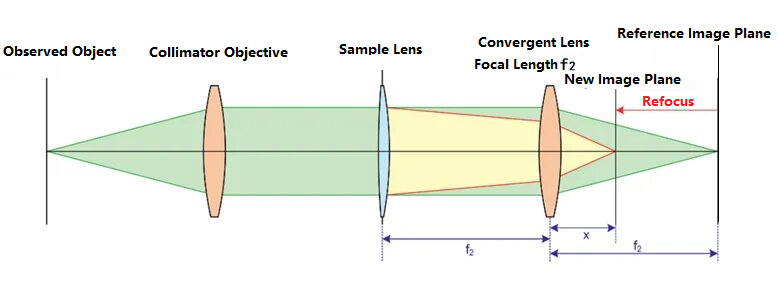
Lensometeret er svært godt egnet for testing av optiske systemer med lang brennvidde. Den skjematiske figuren er som følger:

For det første plasseres ikke linsen som testes i den optiske banen. Det observerte målet til venstre passerer gjennom den kollimerende linsen og blir parallelt lys. Det parallelle lyset konvergeres av en konvergerende linse med en brennvidde på f₂og danner et klart bilde i referansebildeplanet. Etter at den optiske banen er kalibrert, plasseres linsen som testes i den optiske banen, og avstanden mellom linsen som testes og den konvergerende linsen er f₂Som et resultat, på grunn av linsens handling under test, vil lysstrålen bli fokusert på nytt, noe som forårsaker en forskyvning i bildeplanets posisjon, noe som resulterer i et klart bilde på posisjonen til det nye bildeplanet i diagrammet. Avstanden mellom det nye bildeplanet og den konvergerende linsen er betegnet som x. Basert på objekt-bilde-forholdet kan brennvidden til linsen under test utledes som:

I praksis har lensometeret blitt mye brukt i måling av toppfokal på brilleglass, og har fordelene med enkel betjening og pålitelig presisjon.

2.4 AbbeRefraktometer

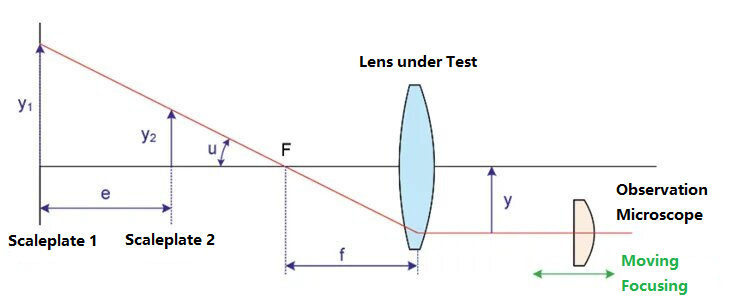
Abbe-refraktometeret er en annen metode for å teste brennvidden til optiske systemer. Den skjematiske figuren er som følger:

Plasser to linjaler med ulik høyde på objektoverflaten av linsen som testes, nemlig skalaplate 1 og skalaplate 2. De tilsvarende høydene på skalaplatene er y1 og y2. Avstanden mellom de to skalaplatene er e, og vinkelen mellom linjalens øverste linje og den optiske aksen er u. Skalaplaten avbildes av den testede linsen med en brennvidde på f. Et mikroskop er installert på bildeflateenden. Ved å flytte mikroskopets posisjon finnes de øverste bildene av de to skalaplatene. På dette tidspunktet er avstanden mellom mikroskopet og den optiske aksen betegnet som y. I henhold til objekt-bilde-forholdet kan vi få brennvidden som:

2.5 Moire-deflektometriMetode
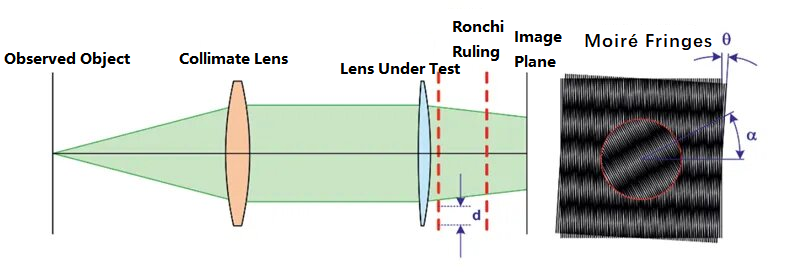
Moiré-deflektometrimetoden bruker to sett med Ronchi-linjer i parallelle lysstråler. Ronchi-linjen er et rutenettlignende mønster av metallkromfilm avsatt på et glasssubstrat, som vanligvis brukes til å teste ytelsen til optiske systemer. Metoden bruker endringen i Moiré-frynser dannet av de to gittrene for å teste brennvidden til det optiske systemet. Det skjematiske diagrammet av prinsippet er som følger:

I figuren ovenfor blir det observerte objektet, etter å ha passert gjennom kollimatoren, en parallell stråle. I den optiske banen, uten å legge til den testede linsen først, passerer den parallelle strålen gjennom to gitter med en forskyvningsvinkel på θ og en gitteravstand på d, og danner et sett med moiré-frynser på bildeplanet. Deretter plasseres den testede linsen i den optiske banen. Det opprinnelige kollimerte lyset, etter refraksjon av linsen, vil produsere en viss brennvidde. Krumningsradiusen til lysstrålen kan fås fra følgende formel:

Vanligvis plasseres linsen som testes svært nær det første gitteret, slik at R-verdien i formelen ovenfor tilsvarer linsens brennvidde. Fordelen med denne metoden er at den kan teste brennvidden til systemer med positiv og negativ brennvidde.

2.6 OptiskFiberAautokollimeringMmetode
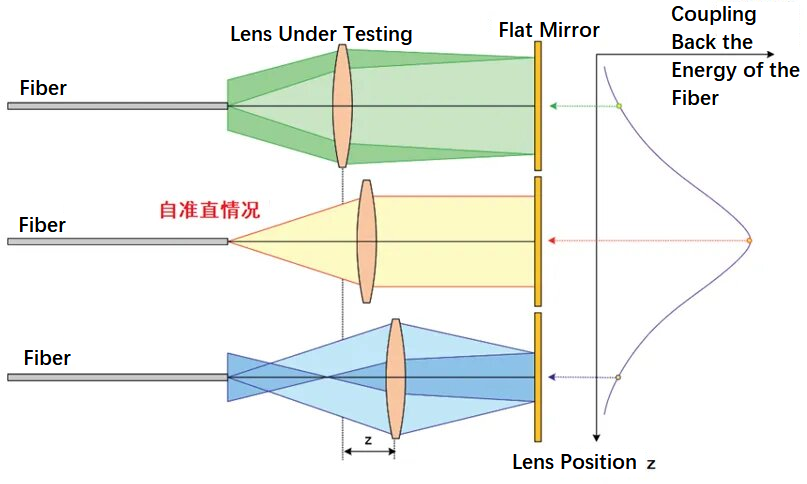
Prinsippet for å bruke autokollimeringsmetoden med optisk fiber for å teste brennvidden til linsen er vist i figuren nedenfor. Den bruker fiberoptikk til å sende ut en divergerende stråle som passerer gjennom linsen som testes og deretter over på et plant speil. De tre optiske banene i figuren representerer forholdene til den optiske fiberen innenfor fokus, innenfor fokus og utenfor fokus. Ved å flytte posisjonen til linsen som testes frem og tilbake, kan du finne fiberhodets posisjon i fokus. På dette tidspunktet er strålen selvkollimert, og etter refleksjon av planspeilet vil mesteparten av energien gå tilbake til fiberhodets posisjon. Metoden er enkel i prinsippet og lett å implementere.

3. Konklusjon

Brennvidde er en viktig parameter i et optisk system. I denne artikkelen beskriver vi konseptet brennvidde for et optisk system og testmetodene dets. Kombinert med det skjematiske diagrammet forklarer vi definisjonen av brennvidde, inkludert konseptene brennvidde på bildesiden, brennvidde på objektsiden og brennvidde foran og bak. I praksis finnes det mange metoder for å teste brennvidden til et optisk system. Denne artikkelen introduserer testprinsippene for kollimatormetoden, Gauss-metoden, brennviddemålingsmetoden, Abbe-brennviddemålingsmetoden, Moiré-avbøyningsmetoden og autokollimeringsmetoden for optisk fiber. Jeg tror at ved å lese denne artikkelen vil du få en bedre forståelse av brennviddeparametrene i optiske systemer.